11. Container With Most Water

MediumLeetCode

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1

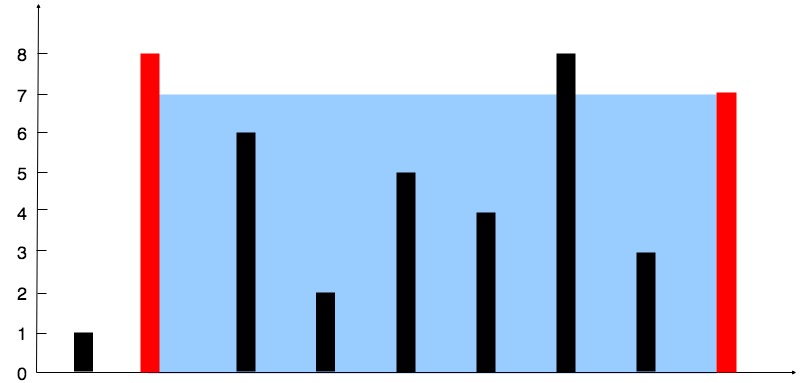
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2

Input: height = [1,1] Output: 1

Constraints

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

How to solve the problem

• Brute Force(O(n^2))

class Solution:
    def maxArea(self, height: List[int]) -> int:
        area = 0
        max_area = 0
        for left in range(len(height)):
            for right in range(len(height)-1, left, -1):
                area = (right - left) * (min(height[left],height[right]))
                max_area = max(area, max_area)
        return max_area

• Two Pointers

python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        area = 0
        max_area = 0
        while left < right:
            area = (right - left) * (min(height[left], height[right]))
            max_area = max(area, max_area)
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
        return max_area

Java

class Solution{
    public int maxArea(int[] height){
        int left = 0, right = height.length - 1;
        int max_area = 0;
        while(left < right){
            int area = Math.min(height[left],height[right]) * (right - left);
            max_area = Math.max(max_area, area);
            if(height[left] < height[right]){
                left ++;
            }else{
                right --;
            }
        }
        return max_area;
    }
}

Complexity

• Brute Force: Time complexity: O(n^2), Space complexity: O(1)
• Two Pointers: Time complexity: O(n), Space complexity: O(1)
  • Each element is visited once, and we only use constant extra space