51. N-Queens

Hard LeetCode

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1

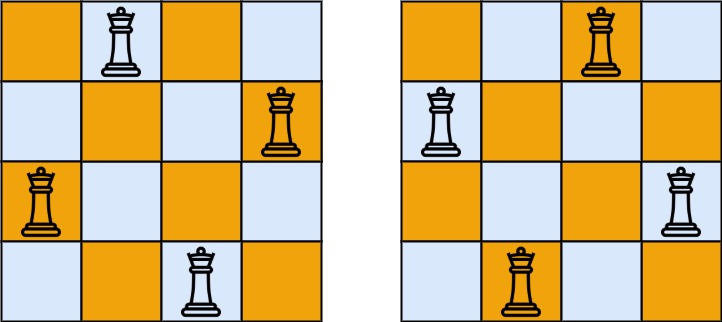
Input: n = 4

Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]

Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2

Input: n = 1

Output: [["Q"]]

Constraints

• 1 <= n <= 9

How to solve the problem

• Backtracking (DFS)

from typing import List

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        solutions = []  # Store all valid board configurations
        queen_columns = [0] * n  # queen_columns[row] gives the column index for the queen in that row

        # Check if placing a queen at (row, col) is valid (no diagonal attacks)
        def is_valid(row, col):
            for prev_row in range(row):  # Check all previous rows
                prev_col = queen_columns[prev_row]  # Column of the queen in the previous row
                # Check for diagonal conflicts
                if row + col == prev_row + prev_col or row - col == prev_row - prev_col:
                    return False  # Conflict detected
            return True  # No conflicts; it's valid

        # Backtracking function to place queens row by row
        def backtrack(row, available_columns):
            if row == n:
                # All queens are placed; construct the board and add to solutions
                board = [
                    '.' * col + 'Q' + '.' * (n - 1 - col) for col in queen_columns
                ]
                solutions.append(board)
                return
            for col in available_columns:  # Try every available column for this row
                if is_valid(row, col):
                    queen_columns[row] = col  # Place queen at (row, col)
                    backtrack(row + 1, available_columns - {col})  # Recurse to next row, removing this column

        backtrack(0, set(range(n)))  # Start from row 0 with all columns available
        return solutions  # Return all the valid solutions

Complexity

• Time complexity: O(n*n!)
• Space complexity: O(n)