654. Maximum Binary Tree

Medium LeetCode

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums. Recursively build the left subtree on the subarray prefix to the left of the maximum value. Recursively build the right subtree on the subarray suffix to the right of the maximum value. Return the maximum binary tree built from nums.

Example 1

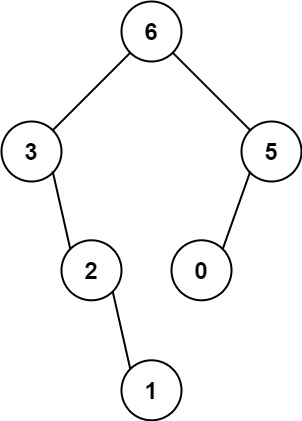
Input: nums = [3,2,1,6,0,5]

Output: [6,3,5,null,2,0,null,null,1]

Explanation: The recursive calls are as follow:

• The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
  • The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
    • Empty array, so no child.
    • The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
      • Empty array, so no child.
      • Only one element, so child is a node with value 1.
  • The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
    • Only one element, so child is a node with value 0.
    • Empty array, so no child.

Example 2

Input: nums = [3,2,1]

Output: [3,null,2,null,1]

Constraints

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• All integers in nums are unique.

How to solve the problem

Code

• Recursion (DFS)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums : # "if nums is None" is incorrect, List nums can be 0 or None
            return None
        max_index = nums.index(max(nums))  # Take the index of max value in nums
        root = TreeNode(nums[max_index])  # Set the max value as root
        root.left = self.constructMaximumBinaryTree(nums[:max_index])
        root.right = self.constructMaximumBinaryTree(nums[max_index + 1:])  # Python slices are left-inclusive but right-exclusive
        return root

Complexity

• Time complexity: O(n), n == number of nodes
• Space complexity: O(n)