98. Validate Binary Search Tree

Medium LeetCode

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key. The right subtree of a node contains only nodes with keys greater than the node's key. Both the left and right subtrees must also be binary search trees.

Example 1

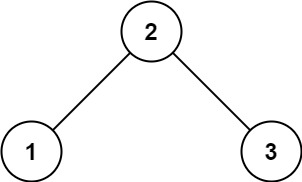
Input: root = [2,1,3]

Output: true

Example 2

Input: root = [5,1,4,null,null,3,6]

Output: false

Explanation: The root node's value is 5 but its right child's value is 4.

Constraints

• The number of nodes in the tree is in the range [1, 104]
• -231 <= Node.val <= 231 - 1

How to solve the problem

Code

• Recursion

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode],left=-inf, right=inf) -> bool:
        if root is None:
            return True
        x = root.val
        return left < x < right and self.isValidBST(root.left, left, x) and self.isValidBST(root.right, x, right)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode], left=-inf, right=inf) -> bool:
        if not root:
            return True
        if not (left < root.val < right):
            return False
        return self.isValidBST(root.left, left, root.val) and self.isValidBST(root.right, root.val, right)

Complexity

• Time complexity: O(n), n == number of nodes
• Space complexity: O(n)