222. Count Complete Tree Nodes

Easy LeetCode

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2^h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example 1

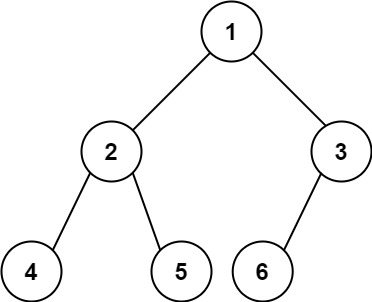
Input: root = [1,2,3,4,5,6]

Output: 6

Example 2

Input: root = []

Output: 0

Example 3

Input: root = [1]

Output: 1

Constraints

• The number of nodes in the tree is in the range [0, 5 * 10^4].
• 0 <= Node.val <= 5 * 10^4
• The tree is guaranteed to be complete.

---

How to solve the problem

Recursion (DFS)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        def dfs(node):
            if node is None:
                return 0
            num_left = dfs(node.left)
            num_right = dfs(node.right)
            return num_left + num_right + 1

        return dfs(root)

• More simplified code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1

Complexity

• Time complexity: O(n), n == number of nodes
• Space complexity: O(n)