94. Binary Tree Inorder Traversal

Easy LeetCode

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Example 1

Input: root = [1,null,2,3]

Output: [1,3,2]

Example 2

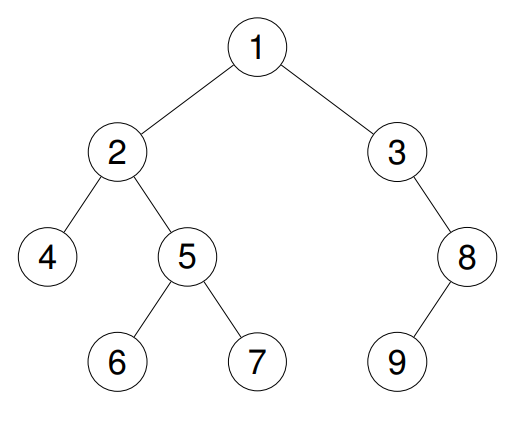
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]

Output: [4,2,6,5,7,1,3,9,8]

Example 3

Input: root = []

Output: []

Example 4

Input: root = [1]

Output: [1]

Constraints

• The number of nodes in the tree is in the range [0, 100]
• -100 <= Node.val <= 100

How to solve the problem

Code

• DFS (Recursion)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # Inorder: Left-Root-Right
        ans = []
        def dfs(node):
            # Determine base case first(stop rucursion)
            if node is None:
                return
            dfs(node.left) # left
            ans.append(node.val) # inorder
            dfs(node.right) # right
        dfs(root)
        return ans

• Iterations with stack

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
         # Inorder: Left-Root-Right
        stack = []
        result = []
        current = root
        while current or stack:
            if current:
                stack.append(current) # Push every node traversed into stack
                current = current.left # Go to the very left node
            else: # when current is None (means left node finished)
                current = stack.pop() # Pop out the current node, the very left one
                result.append(current.val) 
                current = current.right # Then traverse right node
        return result

Complexity

• Time complexity: O(n), n == number of nodes
• Space complexity: O(n)