543. Diameter of Binary Tree

EasyLeetCode

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1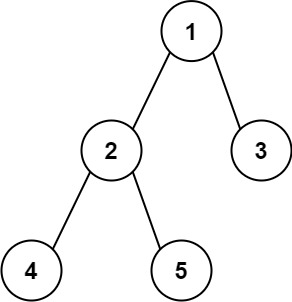

Input: root = [1,2,3,4,5]

Output: 3

Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2

Input: root = [1,2]

Output: 1

Constraints

• The number of nodes in the tree is in the range [1, 10^4].
• -100 <= Node.val <= 100

How to solve the problem

• Depth-First Search (DFS)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# The diameter of a binary tree is the length of the longest path between any two nodes.
# This path may or may not pass through the root.
# For each node, the longest path that passes through it equals the sum of the depths of its left and right subtrees.
# We use DFS to compute the depth of each subtree and update the maximum diameter found.

class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        result = -inf

        def dfs(node):
            if node is None:
                return -1
            l_len = dfs(node.left) + 1  # Length of left subtree
            r_len = dfs(node.right) + 1  # Length of right subtree
            nonlocal result
            result = max(result, l_len + r_len)
            return max(l_len, r_len)

        dfs(root)
        return result  # Return the maximum diameter

Complexity

• Time complexity: O(n)
• Space complexity: O(h)